Action of rotation operators on kets and bras
Rotation operators transform kets and bras by rotating them. A rotation operator \(\hat{R}\) has its adjoint \(\hat{R}^{\dagger}\) which rotates the state just like \(\hat{R}\) but only in the opposite direction. Interestingly, the action of rotation operators on kets and bras are slightly different.
Action of rotation operators on kets
Consider the rotation operator \(\hat{R}\left(\frac{\pi}{2} \mathbf{j}\right)\) acting on the state \(\mid + \mathbf z \rangle\). The operator \(\hat{R}\left(\frac{\pi}{2} \mathbf{j}\right)\) rotates the state \(\mid + \mathbf z \rangle\) about the \(y-\) axis by an angle \(90^\circ\) in the counterclockwise direction, resulting in the new state \(\mid + \mathbf x \rangle\):
\[\begin{equation} \mid + \mathbf x \rangle = \hat{R}\left(\frac{\pi}{2} \mathbf{j}\right) \mid + \mathbf z \rangle. \end{equation}\]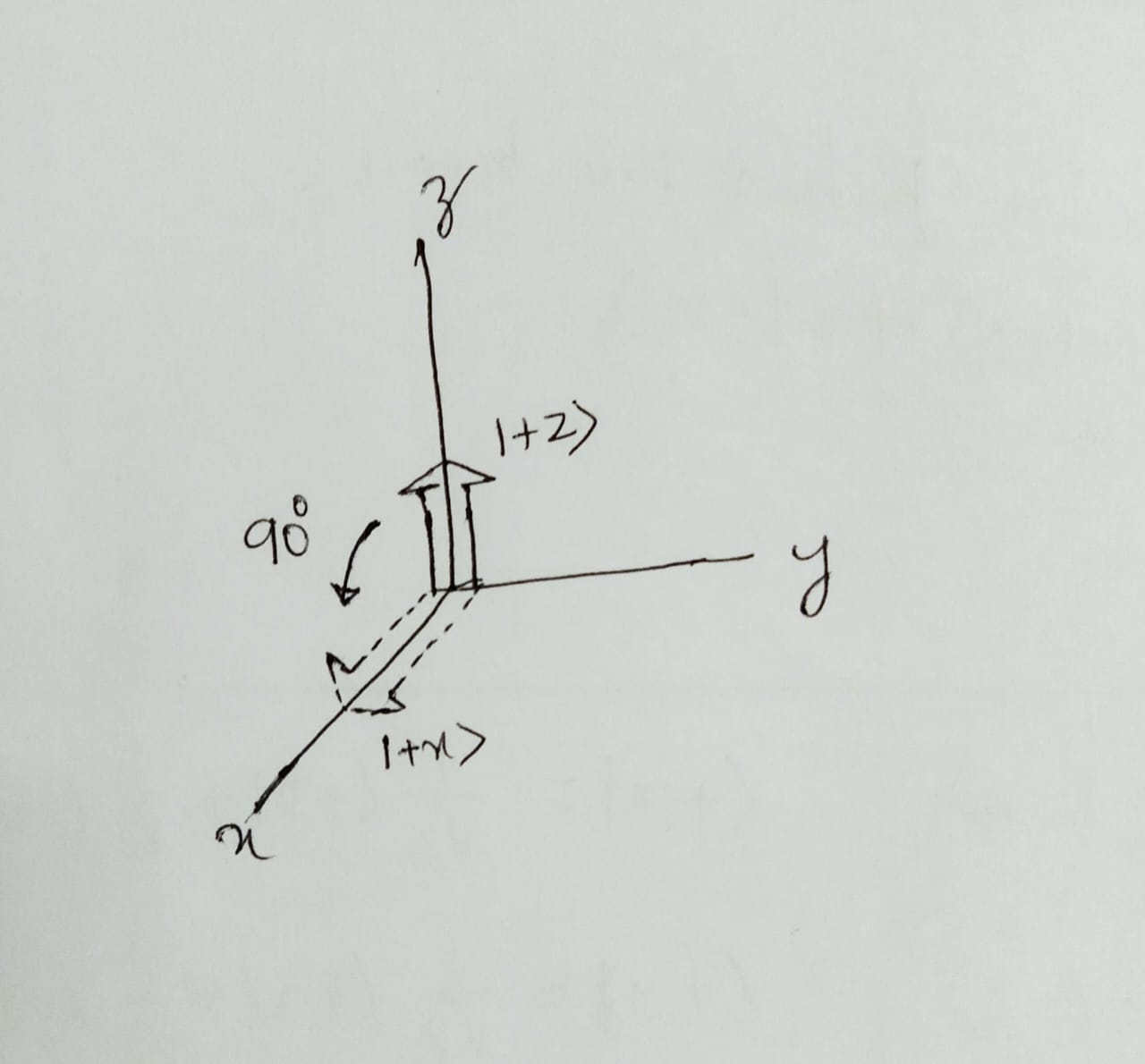
By definition, \(\hat{R}^{\dagger}\left(\frac{\pi}{2} \mathbf{j}\right)\) – adjoint of the operator \(\hat{R}\left(\frac{\pi}{2} \mathbf{j}\right)\) – rotates the ket exactly like \(\hat{R}\left(\frac{\pi}{2} \mathbf{j}\right)\), but in the clockwise direction. Therefore, the action of \(\hat{R}^{\dagger}\left(\frac{\pi}{2} \mathbf{j}\right)\) on \(\mid + \mathbf z \rangle\) results in state \(\mid - \mathbf x \rangle\).
\[\begin{equation} \mid - \mathbf x \rangle = \hat{R}^{\dagger}\left(\frac{\pi}{2} \mathbf{j}\right) \mid + \mathbf z \rangle. \end{equation}\]Action of rotation operators on bras
Since a rotation operator \(\hat{R}\) rotates a ket in the counterclockwise direction, it is tempting to guess that it would do the same for a bra as well. For example, we might think that the action of \(\hat{R}\left(\frac{\pi}{2} \mathbf{j}\right)\) on \(\langle + \mathbf z \mid\) would result in state \(\langle + \mathbf x \mid\):
\[\begin{equation} \langle + \mathbf x \mid = \langle + \mathbf z \mid\hat{R}\left(\frac{\pi}{2} \mathbf{j}\right). \label{eq3} \end{equation}\]Let’s assume that eq. \eqref{eq3} is correct, and see what happens.
We have,
\[\begin{aligned} \langle + \mathbf x \mid + \mathbf x \rangle &= \langle + \mathbf z \mid \hat{R}\left(\frac{\pi}{2} \mathbf{j}\right) \hat{R}\left(\frac{\pi}{2} \mathbf{j}\right) \mid + \mathbf z \rangle \\ &= \langle + \mathbf z \mid \hat{R}\left(\frac{\pi}{2} \mathbf{j}\right) \mid + \mathbf x \rangle \\ &= \langle + \mathbf z \mid - \mathbf z \rangle \end{aligned}\]This is an absurd situation as the LHS is equal to 1 and the RHS is equal to 0.
Therefore, eq. \eqref{eq3} can not be correct. That is, our assumption that the rotation operator \(\hat{R}\) rotates a bra in counterclockwise direction is wrong. Then, \(\hat{R}\) should rotate the bra in clockwise direction and hence \(\hat{R}^{\dagger}\) in counterclockwise direction. Based on this argument, we can write,
\[\begin{equation} \langle + \mathbf x \mid = \langle + \mathbf z \mid\hat{R}^{\dagger}\left(\frac{\pi}{2} \mathbf{j}\right). \label{eq4} \end{equation}\]Eq. \eqref{eq4} goes well with the normalization condition too:
\[\begin{aligned} \langle + \mathbf x \mid + \mathbf x \rangle &= \langle + \mathbf z \mid \hat{R}^{\dagger}\left(\frac{\pi}{2} \mathbf{j}\right) \hat{R}\left(\frac{\pi}{2} \mathbf{j}\right) \mid + \mathbf z \rangle \\ &= \langle + \mathbf z \mid \hat{R}^{\dagger}\left(\frac{\pi}{2} \mathbf{j}\right) \mid + \mathbf x \rangle \\ &= \langle + \mathbf z \mid + \mathbf z \rangle \end{aligned}\]Conclusion
Rotation operators act in different ways on kets and bras. A rotation operator
rotates a ket in counterclockwise direction, but rotates a bra in clockwise
direction. Similarly, the adjoint of the rotation operator rotates a ket in
clockwise direction, but a bra in counterclockwise direction.